学术研究

From: Physically-Accurate Fur Reflflectance: Modeling, Measurement and Rendering.

---

Kajiya-Kay Model

理论

$$S(θ_i,θ_r,ø_i,ø_r)=k_d+k_s\frac{cos^n(θ_r+θ_i)}{cosθ_i}$$

缺陷

Kajiya-Kay模型被设计用于展现纤维散射最重要的特性：垂直于纤维方向的线性高光。虽然多年来这一模型表现良好，但其在多个方面有明显缺陷，首当其冲的是不遵循能量守恒——这对PBR十分重要。

其次,就算在一些情况下物理准确并不重要，Kajiya-Kay模型也无法表达一些现实中观察到的视觉效果，比如透光性。它将纤维视为不透明的圆柱体，并没有考虑到半透明或者内部反射。头发是电介质材质，同时现实中棕色、红色以及其他浅色头发是非常通透的，这是Kajiya模型无法实现的。

Marschner Model

$$\begin{aligned} S\left(\theta_{i}, \theta_{r}, \phi_{i}, \phi_{r}\right) &=\sum_{p} S_{p}\left(\theta_{i}, \theta_{r}, \phi_{i}, \phi_{r}\right) / \cos ^{2} \theta_{d} \\ &=\sum_{p} M_{p}\left(\theta_{h}\right) \cdot N_{p}\left(\phi ; \eta^{\prime}\right) / \cos ^{2} \theta_{d} \end{aligned}$$

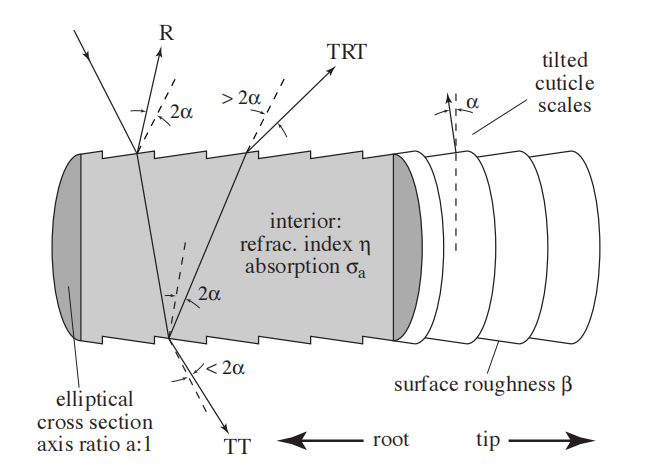
背景

Kajiya-Kay模型的缺陷在上文提及。基于这些不足，Marschner等人基于Kim的模型提出了新的模型。这一模型考虑了：

• Fresnel因子
• 体吸收
• 内部反射
• 对来自不同反射模式的分离高光建模
• 近似了离心效应 ？

测量

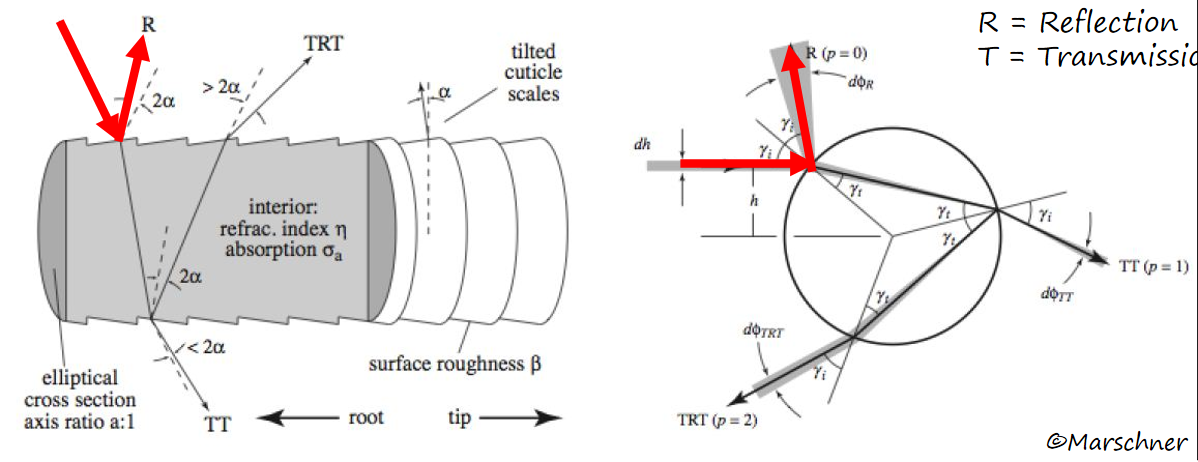
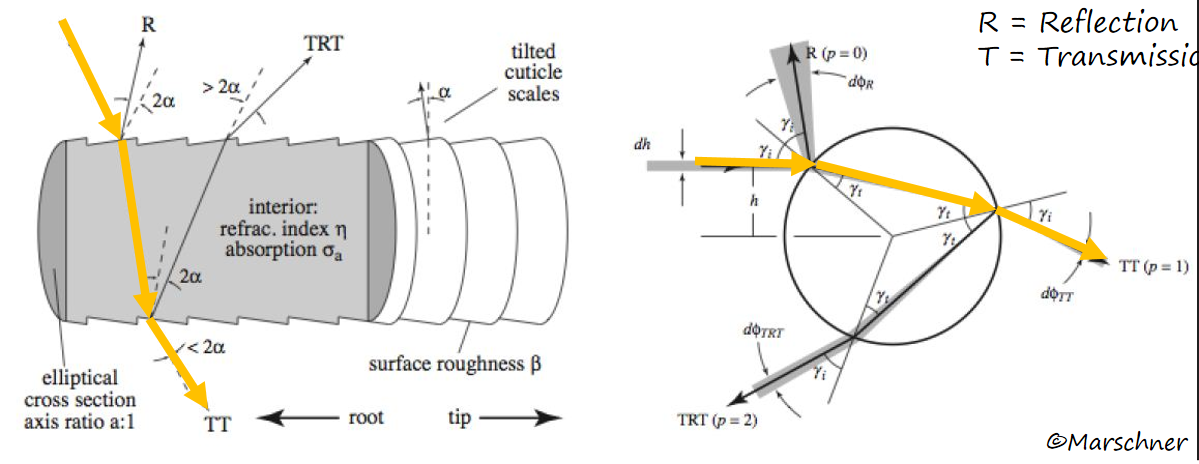
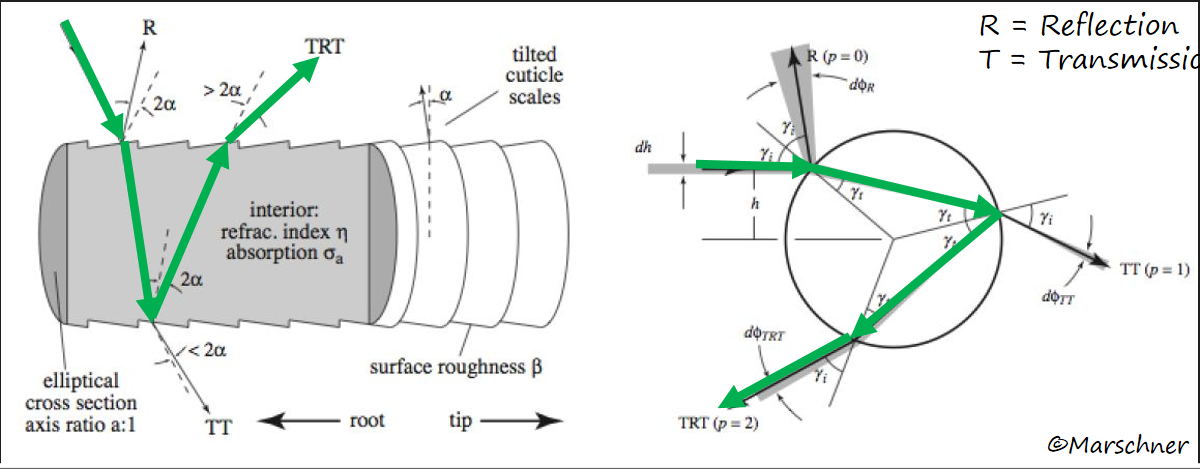
Marschner等人对各种头发进行了测量，以确定在真实物理环境中的高光表现，这一部分细节可以自行看论文第三部分。 通过测量，他们将头发的光照模型分解为三个部分：

• R
  • 光在毛发表面发生镜面反射，是头发高光的主要部分。
  • 来自指向根部的镜面反射，而这一偏差主要源于毛发鳞片的倾斜。
• TT
  • 光入射后从另一方向出射毛发，这一过程中存在一定的散射和吸收。
  • 对于浅色头发而言是很强的前向散射成分，使得金发、棕色、灰色和白色的头发在从后面照射时看起来非常明亮。
• TRT
  • 光入射后，经过一次内部的反射，在从另一边出射。是头发高光的次要部分。
  • 大部分是彩色的，且从白色的主要高光部分向毛发末端方向有一定的偏移。
  • 次要高光随着φ的变化而变化且通常包含两个峰值。峰值位置取决于入射角，并随着θ的增加收敛于入射平面。此外，对于横截面上非圆形的头发，光泽的强度和位置很大程度上取决于头发围绕其轴的旋转角度。这使头发纤维具有独特的闪闪发光的外观。
  • 次要高光中的大部分能量集中在两个峰值中。

理论

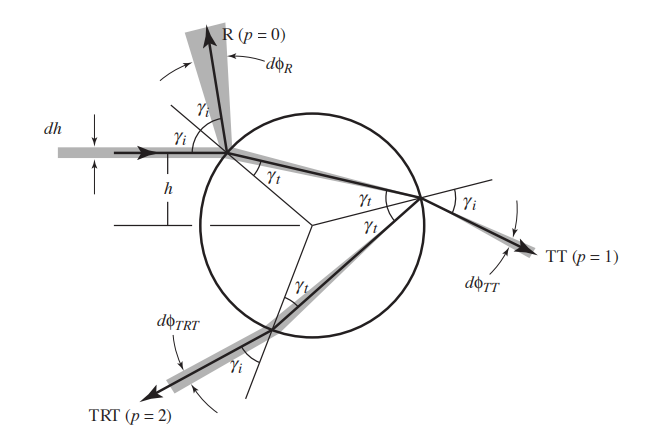
对于柱状的纤维沿着某一轴向时，原有的4D散射方程可以简化为2D参数。

• 以一定角度 γ 入射电解质圆柱的光束，必然以相同的角度出射，无论反射和折射序列如何。
  • 这表示来自 ω 方向的平行入射的射线会产生一组方向位于纤维轴心锥状散射射线。而头发内的折射光方向也同样在一个圆锥体上。这一假设将散射函数从4维降低到了3维，因为散射仅在 θr =－θi 时发生。此等式仅在头发表面粗糙，且头发内没有体积散射的时候近似成立。
• 散射分布对φr的依赖关系可以通过垂直于头发的平面上的投影来分析。
  • 仅从投影中足以计算出R分量。因为3D的镜面反射在2D投影上仍保持为镜面反射。这对折射射线同样适用。所以入射和传输向量投影到一个包含表面法向量的平面上时，仍然符合斯涅尔定律，只是折射率 η 由 折射率函数 η(η, θ)替代了。因此，我们知道所有来自特定入射方向的射线对法平面保持相同的倾斜度，那么在任意折射率的法平面上有效的二维分析就足以描述三维散射函数。 基于这两点得到：

  $$S(φ_i,θ_i; φ_r,θ_r) = M(θ_i,θ_r)N(η' (θ_d); φ_i, φ_r) / cos^2θ_d$$

  这里略去推导过程，最终得到：

$$\begin{aligned} S(φ_i,θ_i;φ_r,θ_r) = M_R(θ_h)N_R(η' (η,θ_d);φ)/cos^2 θ_d +\\ M_{TT} (θ_h)N_{TT} (η' (η,θ_d);φ)/cos^2 θ_d + \\M_{TRT} (θ_h)N_{TRT} (η' (η^∗(φ_h),θ_d);φ)/cos^2 θ_d \end{aligned}$$

其中： 三个M函数是独立的径向散射函数，用于对三种不同模式的角质层进行模拟。 三个N函数是方位散射函数,其中：

$$N_R(φ) = N_p(0,φ)$$

$$N_{T T} (φ) = N_p(1,φ)$$

实现

径向散射函数 M

对于模型的实现有一定的要求，Marschner等人的实现中，理想毛发有如下限制：

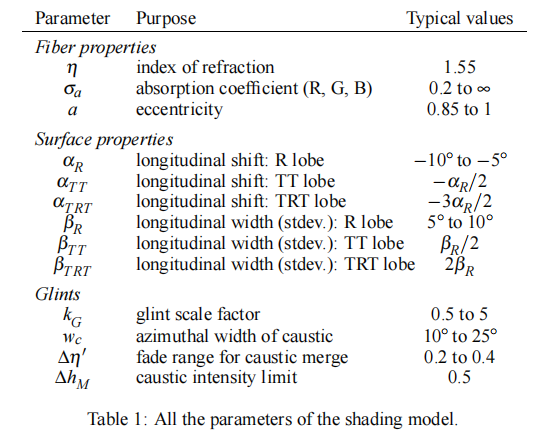
并使用归一化的高斯函数：

$$\begin{aligned} M_{R}\left(\theta_{h}\right) &=g\left(\beta_{R} ; \theta_{h}-\alpha_{R}\right) \\ M_{T T}\left(\theta_{h}\right) &=g\left(\beta_{T T} ; \theta_{h}-\alpha_{T T}\right) \\ M_{T R T}\left(\theta_{h}\right) &=g\left(\beta_{T R T} ; \theta_{h}-\alpha_{T R T}\right) \end{aligned}$$

方位角散射函数 N

略去论文讨论的三种方式，对于R和TT路径的方位角散射，使用以下两式计算：

$$N_{p}(p, \phi)=\sum_{r} A(p, h(p, r, \phi))\left|2 \frac{d \phi}{d h}(p, h(p, r, \phi))\right|^{-1}$$

$$\hat{\phi}\left(p, \gamma_{i}\right)=\left(\frac{6 p c}{\pi}-2\right) \gamma_{i}-\frac{8 p c}{\pi^{3}} \gamma_{i}^{3}+p \pi$$

对于TRT路径，在使用上式计算时，需要带入投影后的折射率：

$$\begin{aligned} \eta_{1}^{*} &=2(\eta-1) a^{2}-\eta+2 \\ \eta_{2}^{*} &=2(\eta-1) a^{-2}-\eta+2 \\ \eta^{*}\left(\phi_{h}\right) &=\frac{1}{2}\left(\left(\eta_{1}^{*}+\eta_{2}^{*}\right)+\cos \left(2 \phi_{h}\right)\left(\eta_{1}^{*}-\eta_{2}^{*}\right)\right) \end{aligned}$$

Weta Digital Model

背景

Marschner等人的模型提供了很好的基础，但是计算复杂难以实现。在此基础上维塔数码和康奈尔大学合作提出PBR头发模型的重要性采样。这篇文章是UE4 Hair着色模型的主要来源。 用于头发渲染的光照模型是BCSDF（ Bidirectional Curve Scattering Distribution Function）

Hair BCSDF Importance Sampling

每个叶的散射公式还是这个：

$$Sp(θ_i, θ_o, φ) = M_p(θ_i, θ_o)N_p(θ_i, θ_o, φ).$$

这里$θ_i$和$θ_o$描述法平面的倾斜度，$φ=φ_o-φ_i$描述入射和出射方向的角度差。

Importance Sampling the Longitudinal M function

对于径向函数:

$$M\left(v, \theta_{\mathrm{c}}, \theta_{o}\right)=\frac{\operatorname{csch}(1 / v)}{2 v} e^{\frac{\sin \theta_{\mathrm{c}} \sin \theta_{0}}{v}} I_{0}\left[\frac{\cos \theta_{\mathrm{c}} \cos \theta_{o}}{v}\right] \frac{1}{\cos \theta_{o}}$$

该M函数的推导是用球面高斯曲线将球面的狄拉克圆$δ(θ−θ_{cone})$进行卷积，然后将该结果的纵向分布作为粗糙度导致的在θ中的扩散。使用$[0,1)$的均匀随机值$ξ_1$和$ξ_2$对$Mcos^2θ_o$做重要性采样。 从球谐高斯方差的重要性采样出发:

$$u\left(\xi_{1}\right)=v \log \left(\mathrm{e}^{1 / v}-2 \xi_{1} \sinh \frac{1}{v}\right)$$

总之，对于给定的方差$v$和镜面锥角$θ_{cone}(θ_i, φ, α)$:

$$\begin{aligned} &\theta_{o}\left(\xi_{1}, \xi_{2}, v, \theta_{\text {cone }}\right)= \\ &\quad \arcsin \left(u\left(\xi_{1}\right) \cos \theta^{\prime}+\sqrt{1-u\left(\xi_{1}\right)^{2}} \cos \left(2 \pi \xi_{2}\right) \sin \theta^{\prime}\right) \end{aligned}$$

其中:

$$θ'=\frac{\pi}{2}-\theta_{cone}$$

这是一个完美的重要性采样，其采样权重为1，PDF为$Mcos^2θ_o$

Importance Sampling the Azimuthal N functions

YanLingQi Model

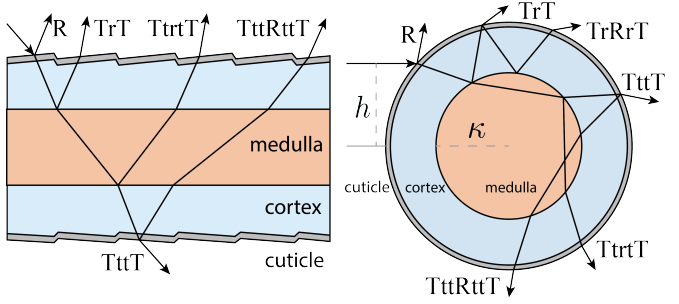
在Marschner的模型基础上,Yan等人对头发做了更进一步的模型,考虑了发髓（Medulla）、皮层(Cortex）以及外皮（Cuticle）。

闫大佬的文章写得很好，大家自己看看吧，此处略过。。。。。

引擎实现

ATI 2004 Siggraph

原理部分

模型要求

在Marschner发表之后，ATI实现了一个混合了Kajiya和Marschner模型的Demo，也是如今大部分头发着色的技术来源。

• 用多层面片去近似头发的体积
• 使用AO近似自阴影

纹理

• BaseColor包含alpha通道用于表示发梢部分
• SpecularShift纹理和SpecularNoise纹理

光照模型 Kajiya

• 各向异性光照模型、
• 在光照方程中使用切线而不是法线
• 假设头发法线位于T和视线方向V的夹平面上

$$sin(T,H)^{specularity}={\sqrt{1-dot(T,H)^2}}^{specularity}$$

光照模型 Marschner

• ATI觉得数学过于复杂，所以只近似一下表现就好
• 其实还是主要高光和次要高光这些东西
• 以及次要高光的闪烁

实现细节

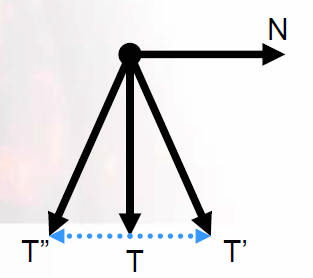
Shifting Specular Highlight

• 在$N$方向上稍微抖动一下$T$
• 假设$T$从发根指向发梢
• 使用ShiftTexture控制如何抖动，以0.5为原点，小于0.5则向$N$的反方向偏移，反之亦然。

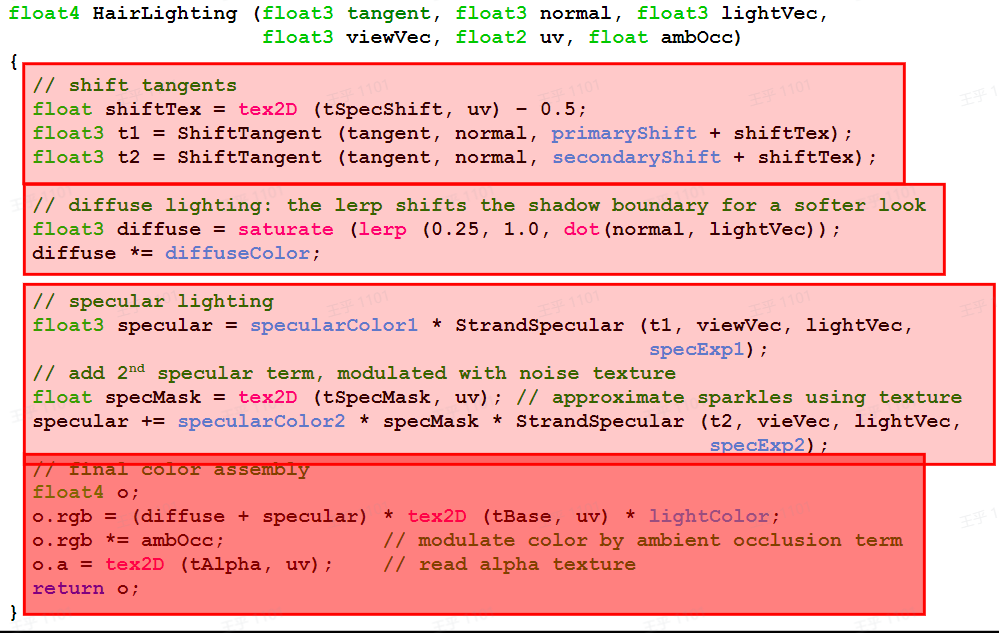
Specular Strand Lighting

• 使用半角向量计算发丝的光泽
• 两层高光有不同的颜色、光泽和切线
• 使用噪声纹理扰动次级高光
• dirAtten值是通过方向控制Kajiya-Kay 着色模型中可见高光范围的衰减系数，即通过切线向量T和Half向量H的夹角的角度的不同，控制所得的高光能量值

半透明物体排序

受限于当时的硬件，头发有半透明排序的问题，ATI使用了4个Pass优化整个头发的渲染，参考一下原文档即可。

Epic 2016 Siggraph

原理和背景

2016年，Epic在Siggraph上有一个演讲详细描述了UE对毛发渲染的实现。 原理还是基于以上Marschner和Weta的论文，对R、TT、TRT部分各自做了近似和计算。

实时的Marschner模型难以实现，需要一些改动和近似。

Epic的近似

Longitudinal Scattering Function

weta的能量守方程过于昂贵，所以使用高斯函数近似。 其中有α和β两个参数：

• α基于角质层鳞片的倾斜度
• β基于毛发的粗糙度

Azimuthal Scattering Fucntion

Azimuthal R

方位角的散射方程有一些处理，首先R路径的计算比较简单：

$$N_R(θ_i ,θ_r,ϕ)=(\frac{1}{4}cos\frac{ϕ}{2})A(0,ℎ)$$

其中：

$$A(0,ℎ)=F(η,\sqrt{\frac{1}{2}+\frac{1}{2}(ω_i∙ω_r) })$$

$$cos\frac{ϕ}{2}=\sqrt{\frac{1}{2}+\frac{1}{2}cosϕ}$$

$$F(η,x )=F_0+(1−F_0)(1−x)^5$$

$$F_0=(1−η)^2/(1+η)^2$$

效果也还行：左参考，右近似

Other Azimuthal Path

然而其他路径并没那么容易：

$$N_p(θ_i ,θ_r,ϕ)=\frac{1}{2}∫_{−1}^1A(p,ℎ)D_p(ϕ−Φ(p,ℎ))dℎ$$

其中：

• 衰减项

$$A(p,ℎ)=(1−f)^2f^{p−1}T(μ_a,ℎ)^p$$

$$f=F(η,cos(θ_d)\sqrt{1−ℎ^2})$$

• 吸收项

$$T(μ_a,ℎ)=exp⁡(−2μ_a\frac{1+cos(2γ_t)}{cosθ_t})$$

Azimuthal TT

由上式，准确的TT偏移量h应该是：

$$a=\frac{1}{η^′}$$

$$ℎ_{TT}=\frac{sign(ϕ)cos\frac{ϕ}{2}}{\sqrt{1+a^2−2a sign(ϕ)sin\frac{ϕ}{2}}}$$

三角变换一下：

$${ℎ_{TT}}^2=\frac{\frac{1}{2}+\frac{1}{2}cosϕ}{1+a^2−2a\sqrt{\frac{1}{2}−\frac{1}{2}cosϕ}}$$

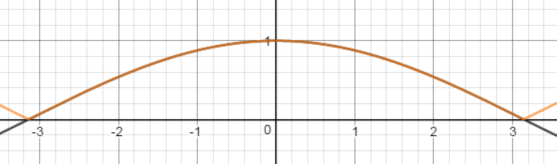
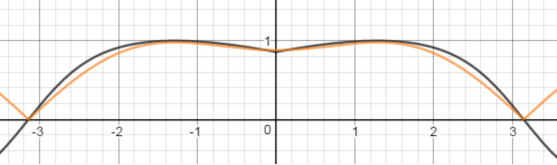
下面是α=0和α=0.6时的分布曲线：

当然这样的计算还是很高昂，遇事不决，来亿点点近似：

$$ℎ_{TT}≈(1+a(0.6−0.8cosϕ)cos\frac{ϕ}{2}$$

对于折射率，原有公式长这样：

$$η^′=\frac{\sqrt{η^2−sin^2θ_d} }{cosθ_d}$$

也需要一些近似：

$$η=1.55$$

• 源于Marshner的原始论文

$$η^′≈\frac{1.19}{cosθ_d}+0.36cosθ_d$$

• error<0.68%

对于吸收项，公式如下：

$$T(θ,ϕ)=exp(−2μ_a\frac{1+cos(2γ_t)}{cosθ_t})$$

$$γ_t=sin^{−1}(\frac{ℎ}{η^′})$$

替换为Pixar的吸收项：

$$T(θ,ϕ)=exp⁡(−ζ(C)\frac{cosγ_t}{cosθ_d})$$

• 其中C为头发的BaseColor

代入

$$γ_t=sin^{−1}(\frac{ℎ}{η^′})$$

有：

$$T(θ,ϕ)=C^{\frac{\sqrt{1−ℎ^2a^2}}{2cosθ_d}}$$

关于D项，从Pixar的分布函数近似出发：

$$D(ϕ,s,μ)=\frac{e^{\frac{ϕ−μ}{s}}}{s(1+e^\frac{ϕ−μ}{s})^2}$$

Epic再来亿个近似：

$$D_{TT}(ϕ)=D(ϕ,0.35,π)$$

$$D_{TT}(ϕ)≈e^{−3.65cosϕ−3.98}$$

Azimuthal TRT

Marschner对TRT的求解得到h项有多解，这表示有多个高光叶。 weta通过数值积分求解。 Pixar通过一个非常大的查找表求解。 Epic通过粗暴简化求解：

对于h 项，出于Fresnel的考虑：

$$ℎ_{TRT}=\frac{\sqrt3}{2}$$

对于吸收项：

$$T_{TRT}(θ,ϕ)=C^\frac{0.8}{cosθ_d}$$

对于分布函数:

$$D_{TRT}(ϕ)=\frac{3}{4}D(ϕ,0.15,0)$$

$$D_{TRT}(ϕ)≈e^{17cosϕ−16.78}$$

整体对比

还是丢失了点啥。。。 多重散射 对于浅色头发来说，头发体积内的多重散射十分重要，仅仅单次计算单根头发内的光线是不够的。 但是呢，有一些困难

• 实时路径追踪想都别想
• 需要研究如何简化双重散射
• 没有时间制作一个PathTracing的参考了
• 所以只能用简单的模型代替

所以最终的结果是：

• 使用FakeNormal代替法线：

$$n=\frac{ω_r−u(u∙ω_r)}{‖ω_r−u(u∙ω_r)‖}$$

• 阴影在ShadowMap中指数级衰减
• 直接光的吸收使用阴影作为路劲长度

$$S_{scattering}=\sqrt{C}(\frac{n∙ω_i+1}{4π})(\frac{C}{Luma})^{(1−Sℎadow)}$$

美术参数

至此，UE4方案中的参数解释如下：

• BaseColor
  • C in equations
• Specular
  • Scales the R term
• Roughness

  • $$β_R=Rougℎness^2$$

  • $$β_{TT}=0.5 Rougℎness^2$$

  • $$β_{TRT}=2 Rougℎness^2$$

• Scatter
  • Scales multiple scattering term
• Shift

  • $$α_R=−2 Sℎift$$

  • $$α_{TT}=Sℎift$$

  • $$α_{TRT}=4 Sℎift$$

阴影

阴影对头发的表现至关重要，在Epic的方案中，阴影有以下要点：

• 使用ShadowMap，PCF滤波
• 指数衰减
• 体积
• 没有球形法线
• 对于没有阴影的光源，使用平面空间阴影
  • 在屏幕空间深度Buffer中使用光线投射（Ray Cast）

环境光

• 在假法线方向上采样环境照明的球谐函数，并将其视为定向光源。
  • 乘上 $$π$$
• 使用修改后的BSDF
  • R 乘以 $$saturate(ω_i∙ω_r+1)$$
  • 移除 TT
  • 对每个$$β$$加上$$0.2$$
• 由于没有阴影，需要修改BSDF
  • 不想要锃光瓦亮的头
  • 屏幕空间的弯曲锥体可能会解决这一问题

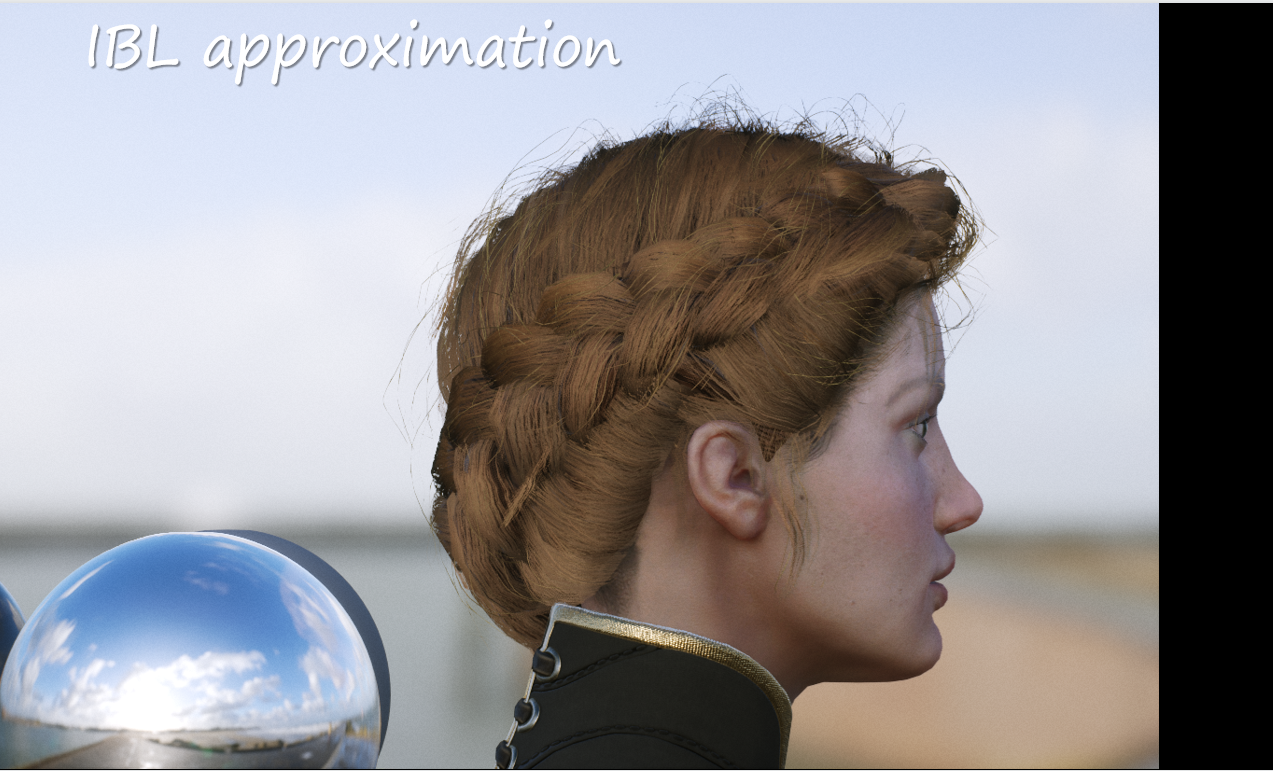UE4.27 源码

源码入口

所有着色模型的入口都在

• Engine/Shaders/Private/ShadingModels.ush 根据BxDF的调用和#Include，HairShading主要代码在
• Engine/Shaders/Private/HairBsdf.ush
• 注意Epic在这里保留了HairShading和HairShadingRef两种着色。
• 为了突出，这里省略了一些无关的注释和分支，有兴趣可以看源码。
• 对R，TT，TRT部分计算之后，如果是多重散射的情况，Epic直接使用多重散射和KajiyaKay漫反射。

核心代码

float3 HairShading( FGBufferData GBuffer, float3 L, float3 V, half3 N, float Shadow, FHairTransmittanceData HairTransmittance, float InBacklit, float Area, uint2 Random )
{
   float ClampedRoughness = clamp(GBuffer.Roughness, 1/255.0f, 1.0f);
   const float Backlit    = min(InBacklit, HairTransmittance.bUseBacklit ? GBuffer.CustomData.z : 1);

   // N is the vector parallel to hair pointing toward root
   const float VoL       = dot(V,L);                                                      
   const float SinThetaL = clamp(dot(N,L), -1.f, 1.f);
   const float SinThetaV = clamp(dot(N,V), -1.f, 1.f);
   float CosThetaD = cos( 0.5 * abs( asinFast( SinThetaV ) - asinFast( SinThetaL ) ) );


   const float3 Lp = L - SinThetaL * N;
   const float3 Vp = V - SinThetaV * N;
   const float CosPhi = dot(Lp,Vp) * rsqrt( dot(Lp,Lp) * dot(Vp,Vp) + 1e-4 );
   const float CosHalfPhi = sqrt( saturate( 0.5 + 0.5 * CosPhi ) );

   float n = 1.55;
   float n_prime = 1.19 / CosThetaD + 0.36 * CosThetaD;

   float Shift = 0.035;
   float Alpha[] =
   {
      -Shift * 2,
      Shift,
      Shift * 4,
   }; 
   float B[] =
   {
      Area + Pow2(ClampedRoughness),
      Area + Pow2(ClampedRoughness) / 2,
      Area + Pow2(ClampedRoughness) * 2,
   };

   float3 S = 0;
   
   // R
   if (HairTransmittance.ScatteringComponent & HAIR_COMPONENT_R)
   {
      const float sa = sin(Alpha[0]);
      const float ca = cos(Alpha[0]);
      float Shift = 2 * sa * (ca * CosHalfPhi * sqrt(1 - SinThetaV * SinThetaV) + sa * SinThetaV);
      float BScale = HairTransmittance.bUseSeparableR ? sqrt(2.0) * CosHalfPhi : 1;
      float Mp = Hair_g(B[0] * BScale, SinThetaL + SinThetaV - Shift);
      float Np = 0.25 * CosHalfPhi;
      float Fp = Hair_F(sqrt(saturate(0.5 + 0.5 * VoL)));
      S += Mp * Np * Fp * (GBuffer.Specular * 2) * lerp(1, Backlit, saturate(-VoL));
   }

   // TT
   if (HairTransmittance.ScatteringComponent & HAIR_COMPONENT_TT)
   {
      float Mp = Hair_g( B[1], SinThetaL + SinThetaV - Alpha[1] );

      float a = 1 / n_prime;
      float h = CosHalfPhi * ( 1 + a * ( 0.6 - 0.8 * CosPhi ) );
      float f = Hair_F( CosThetaD * sqrt( saturate( 1 - h*h ) ) );
      float Fp = Pow2(1 - f);

      float3 Tp = 0;
      if (HairTransmittance.bUseLegacyAbsorption)
      {
         Tp = pow(GBuffer.BaseColor, 0.5 * sqrt(1 - Pow2(h * a)) / CosThetaD);
      }
      else
      {
         const float3 AbsorptionColor = HairColorToAbsorption(GBuffer.BaseColor);
         Tp = exp(-AbsorptionColor * 2 * abs(1 - Pow2(h * a) / CosThetaD));
      }

      float Np = exp( -3.65 * CosPhi - 3.98 );

      S += Mp * Np * Fp * Tp * Backlit;
   }

   // TRT
   if (HairTransmittance.ScatteringComponent & HAIR_COMPONENT_TRT)
   {
      float Mp = Hair_g( B[2], SinThetaL + SinThetaV - Alpha[2] );
      
      //float h = 0.75;
      float f = Hair_F( CosThetaD * 0.5 );
      float Fp = Pow2(1 - f) * f;
      //float3 Tp = pow( GBuffer.BaseColor, 1.6 / CosThetaD );
      float3 Tp = pow( GBuffer.BaseColor, 0.8 / CosThetaD );

      //float s = 0.15;
      //float Np = 0.75 * exp( Phi / s ) / ( s * Pow2( 1 + exp( Phi / s ) ) );
      float Np = exp( 17 * CosPhi - 16.78 );

      S += Mp * Np * Fp * Tp;
   }

   if (HairTransmittance.ScatteringComponent & HAIR_COMPONENT_MULTISCATTER)
   {
      S  = EvaluateHairMultipleScattering(HairTransmittance, ClampedRoughness, S);
      S += KajiyaKayDiffuseAttenuation(GBuffer, L, V, N, Shadow);
   }

   S = -min(-S, 0.0);
   return S;
}

材质使用

SuperStar的头发材质

SuperStar第一阶段没有使用GroomHair，而是采用传统的头发模型，所以材质比较简单，只是使用了一张各项异性纹理，用于扰动切线和Roughness，以提升头发的质感。

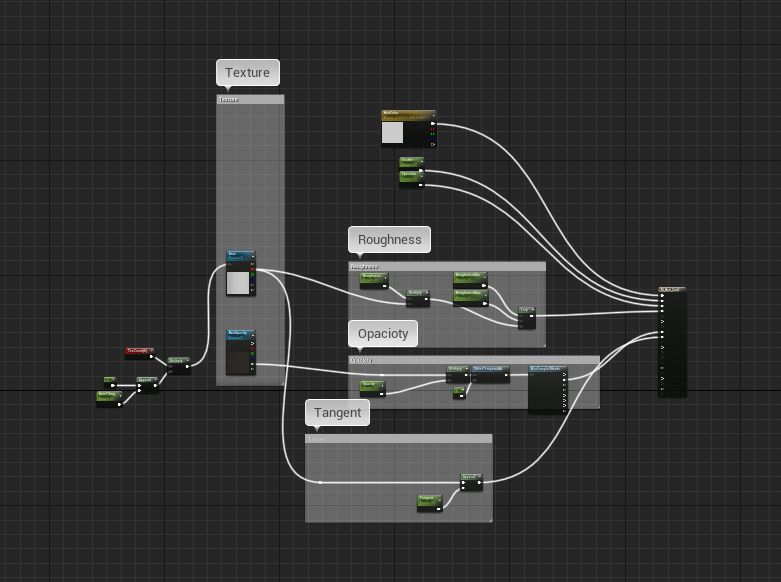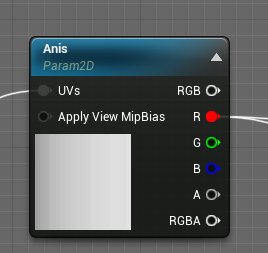MetaHuman的头发材质

对于Groom头发，可以使用HairAttributes获取每根头发的详细参数。光照模型已经在底层实现了，所以材质节点中主要是功能性的计算。

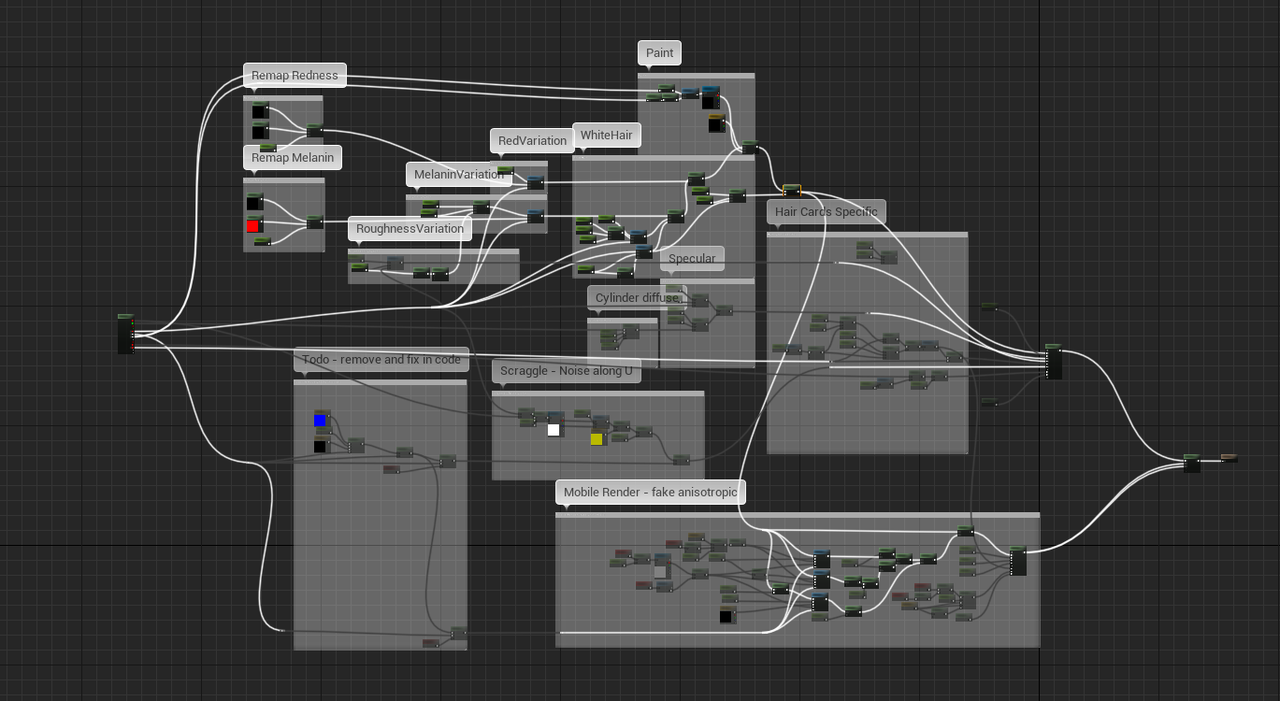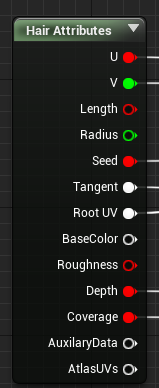BaseColor

BaseColor中的主要有Paint（彩绘），Redness（红色素），Melanin（黑色素）控制。

• Paint部分利用RootUV采样纹理
• Redness部分对原始输入的参数重新映射到材质参数集设置的范围，并使用Variation节点的处理
• Melanin部分采用类似Redness的操作，只不过多了使用Roughness插值的过程。
• 在White部分，对以上两参数处理之后作为HairColor节点的输入得到白色头发分布，并最终和Paint的结果混合。 这里注意Variation节点,其本质为：

$$R = L(S^{v+1},S,S^{\frac{1}{v+1}},P)$$

$$L(a_1,a_2,a_3,A)=lerp(lerp(a_1,a_2,2A),a_3,2A-1)$$

Scatter

MH的材质中并没有Scatter参数，此项没有作用。

Roughness

对Roughness的操作很简单，只有简单的Variation而已。

Opacity

从Hair的材质参数中获取到Coverage，这里使用了ShadowPassSwitch，用于控制材质在写入阴影Pass时的数据。

• 常规渲染下，使用WorldUnitsInPixel获取屏幕像素大小，用于差值远近不同的透明度。最终使用DitherTemporalAA得到透明度。
• 在ShadowPass中，则直接使用Coverage写入。

Tangent

通过一些莫名其妙的诡异操作得到一个向量。。。。

Pixel Depth Offset

这一步通过深度和抖动偏移像素。此项没有作用或不明显。

移动端优化

MH的头发材质自带一个用于移动端的默认光照版本，提供近似的各向异性。后续整理。

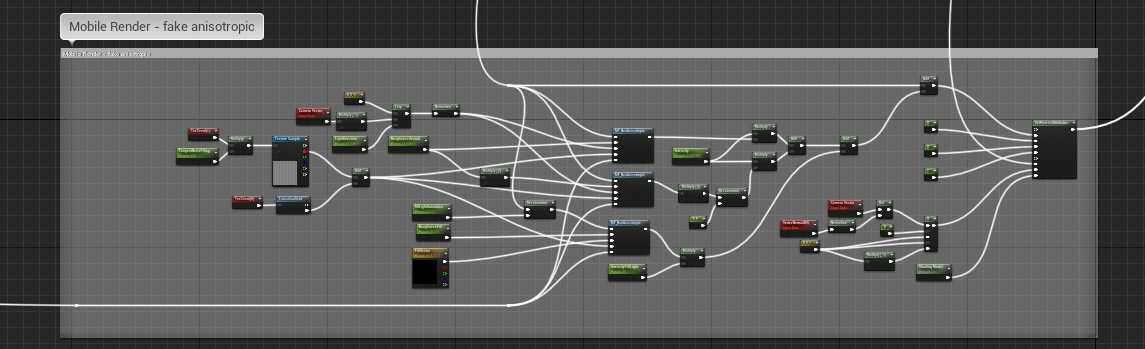参考文档

• 剖析Unreal Engine超真实人类的渲染技术Part 3 - 毛发渲染及其它 - 0向往0 - 博客园
• 照片级角色 | 虚幻引擎文档
• Real-Time Volumetric Shadows | A GSoC 2011 Crystal Space project
• Real-Time Hair Simulation and Rendering | A GSoC 2010 Crystal Space project
• Unreal Engine 4 —— Pixel Depth Offset的使用心得_痞子龙3D编程-CSDN博客

参考论文/PPT

• 2013_hairbrief.pdf
• hair-sg03final.pdf
• Physically-Accurate Fur Reflectance.pdf
• s2016_pbs_epic_hair.pptx
• Scheuermann_HairRendering.pdf